We explore the attention mechanism used in sequence to sequence networks. Let’s go!

Neural Machine Translation

It’s 2014 and we begin with the task of Neural Machine Translation (NMT). Unlike statistical machine translation, NMT aims at building a single neural network that can be jointly learned to maximize the translation performance. These models generally have an encoder-decoder architecture where the encoder converts the input sequence to a fixed length vector, which the decoder uses as its context for generating the output sequence.

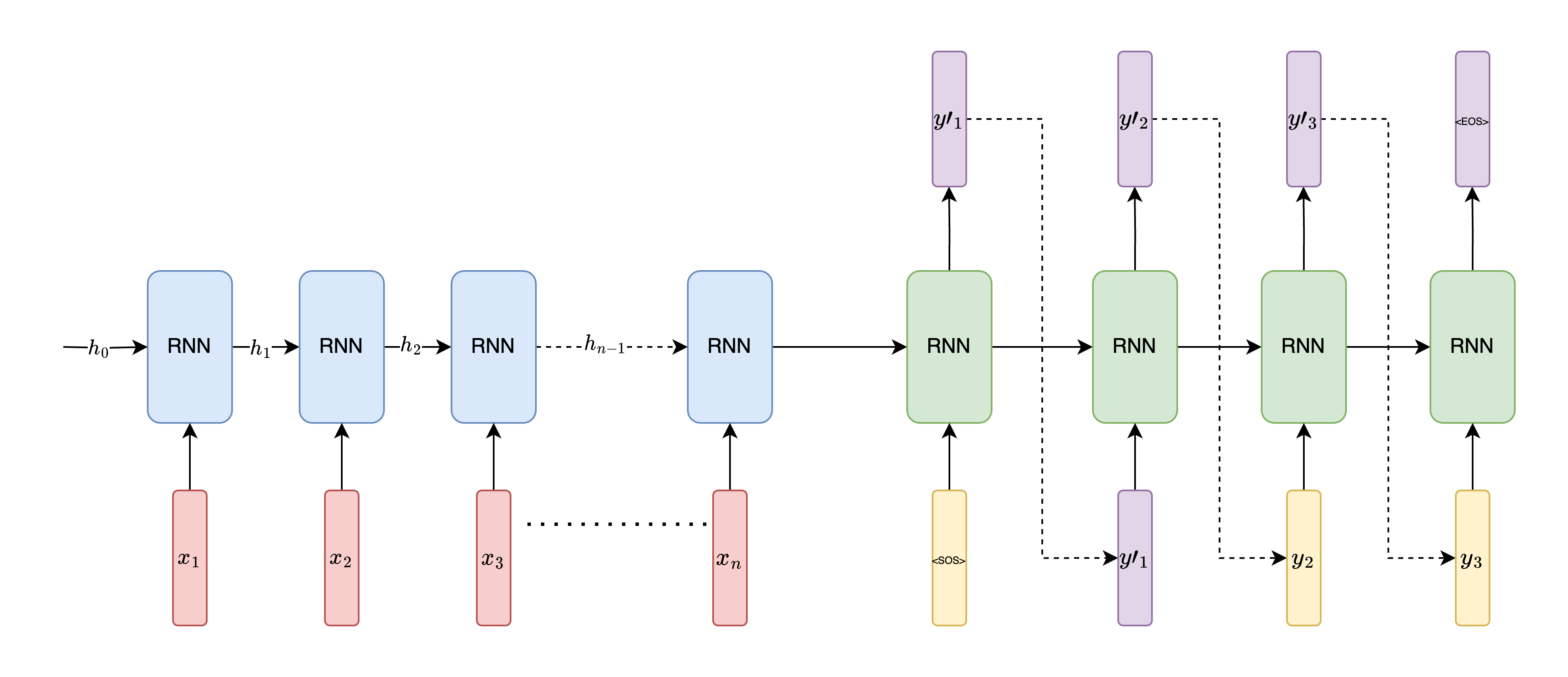
Encoder-Decoder architecture for neural machine translation

Here, the encoder units are in blue, decoder units in green, input sequences in red and output sequences in purple. Input \(x_{0}, x_{1} ... x_{n}\) is fed sequentially to the encoder with the output of the encoder at time \(t_{n}\) depending on hidden state \(h_{n-1}\) and input \(x_{n}\). The output of the encoder \(h_{n}\) or \(s_{0}\) captures the input as a fixed length vector and is fed as input to the decoder. The decoder generates the first output token given \(s_{0}\) and <sos> token. The output of the decoder at \(t_{1}\) ie. \(y^{`}_{1}\) is fed as input to the decoder at time step \(t_{2}\) along with the previous hidden state. This is done till a <eos> token is generated. Now, during training, the generated input can be gibberish, so we need a good way to compute the loss and train the network. Instead of providing the previous time-step output, we provide the ground-truth label \(y_{i-1}\) as input for time-step \(t_{i}\).

The drawback of compressing all of the input information in a fixed length vector is that the network fails to perform well for long sentences. The performance deteriorates rapidly as the length of the sentence increases .

Attention-based Models

Attention-based models address the above problem by looking at the entire input sequence before generating a new word. As mentioned in , each time the model generates a new word, it (soft-)searches for a set of positions in a source sentence where most relevant information is concentrated. The model then predicts the target word based on the context vectors and the previous generated target word. This is shown in the figure below (blue block). Let’s explore this a bit.

Encoder-Decoder architecture with attention

Attention block

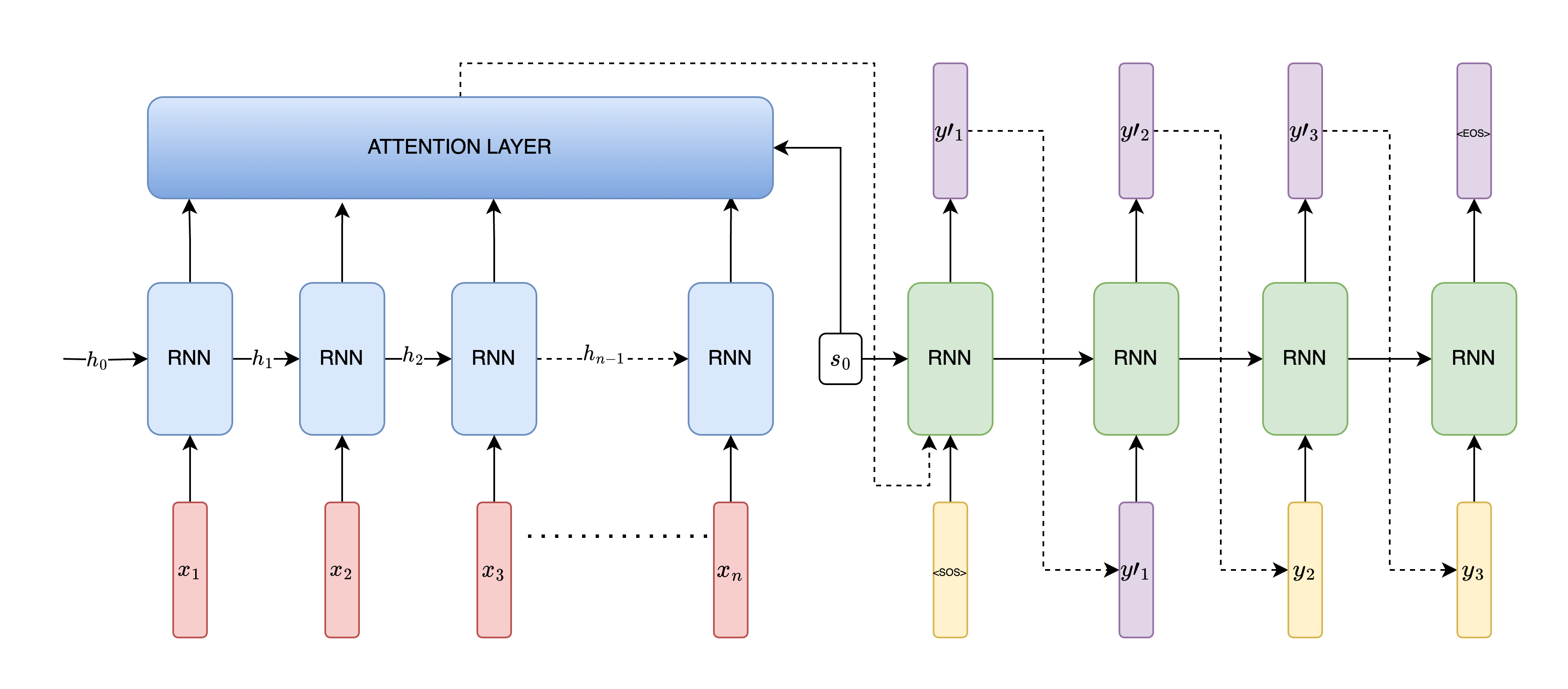
Let’s explore the attention block in a bit more detail. The inputs to this block while decoding at time \(t\) are the encoder hidden states \((h_1, h_2, ... h_n)\) and the previous decoder hidden state \(s_{t-1}\). The output is a context-vector \(c_t\) which is input along with the input token to the decoder. This is shown in the figure below

Fig. Attention block

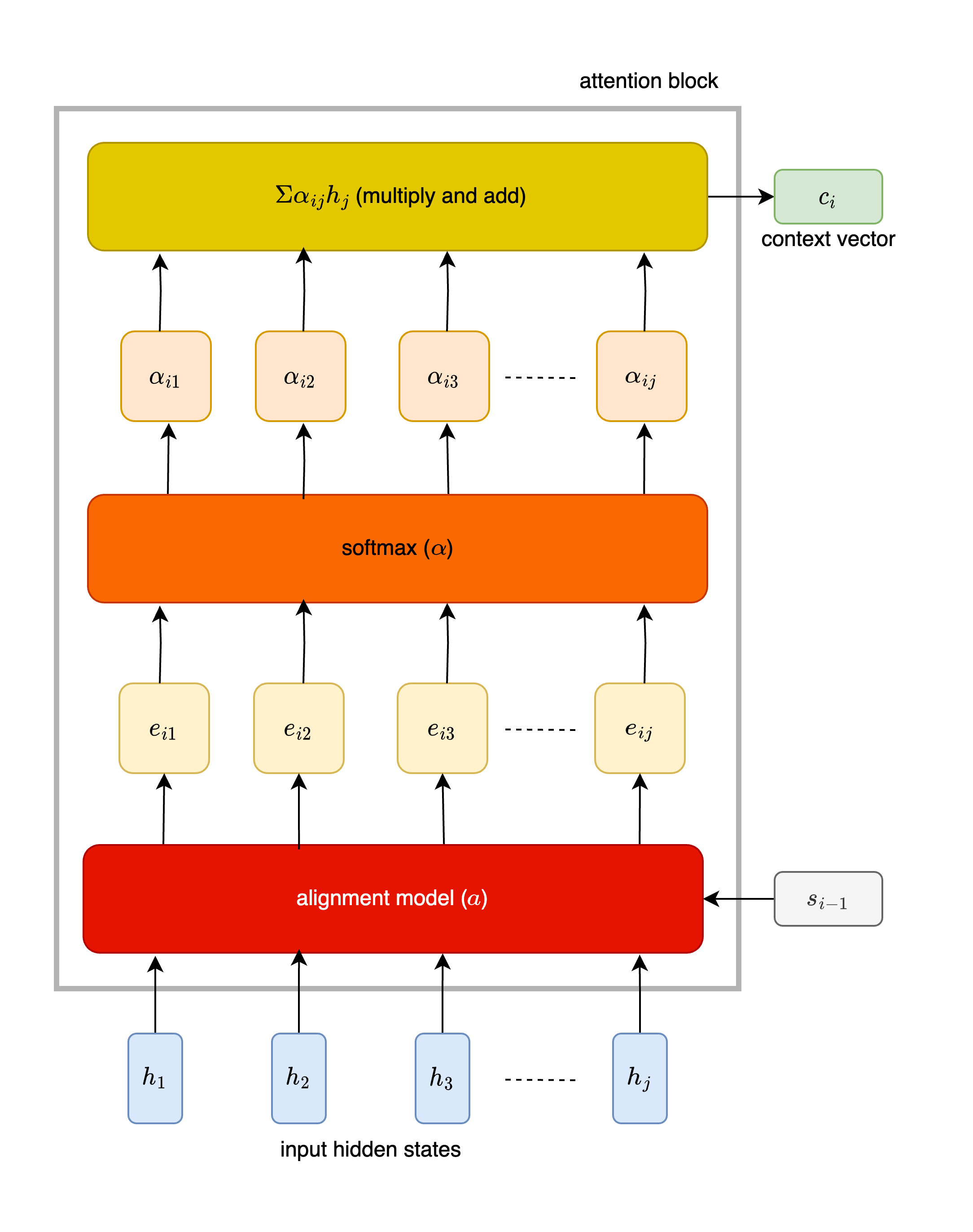
First, we compute scores (\(e_{ij}\)) using the alignment model.

\begin{equation} e_{ij} = a(s_{j-1}, h_j) \end{equation}

It tells us how well the inputs around position \(j\) and the output at position \(i\) match. Then we pass the scores through a softmax function to compute the weight \(\alpha_{ij}\) of each \(h_j\).

\begin{equation} \alpha_{ij} = \dfrac{exp(e_{ij})}{\sum_{k=1}^{T_x} exp(e_{ik})} \end{equation}

The context vector \(c_i\) is then computed as the weighted sum of the annotations \(h_i\)

\begin{equation} c_i = \sum_{j=1}^{T_x} \alpha_{ij} h_i \end{equation}

Although in the diagram above, we show only for one context vector, this operation is done for each step of the decoder generation phase. Section 3.1 of has in detail description of what these values mean and how one can intuitively think of them.

Global v/s Local attention

In , the authors explore two different types of attention mechanisms. When you attend to all the words in the input, its called global or soft attention. On the other hand, when the attention mechanism focuses on a small window of context, its called local attention. Hard attention is a modification to local, where the window size is one ie. we focus only on one hidden state to generate the context vector. While less expensive during inference, the hard attention model is non-differentiable and requires more complicated techniques such as variance reduction or reinforcement learning to train. We will explore this topic in detail later.

Self-Attention

One of the most important building block leading up-to the transformer is self-attention introduced by in 2017 as a way to replace the max pooling or averaging step in sequential models. Instead of a single vector representation, this mechanism is performed on top of a sequence model extracting multiple vector representations based on the hidden states of the LSTM. This is explained with an example (Fig. 1) as follows from . Of the two parts in this model, the first is a bidirectional LSTM (not covered here) and the second is the self-attention mechanism which we will cover in detail (section 2.1 of the paper).

Let the sentence S have n tokens represented by their embeddings \(w_i\) which is a d dimensional vector. Thus S can be represented as matrix with dimension \(n \times d\). Let \(h_i\) be the concatenated hidden state of the LSTM with 2u dimensions. Therefore, H is a matrix of size \(n \times 2u\).

\begin{equation} S = (w_1, w_2, … , w_n) \end{equation}

\begin{equation} H = (h_1, h_2, … , h_n) \end{equation}

Fig. Input embedding and LSTM hidden vectors

The aim is to encode this variable sequence into a fixed size embedding. Unlike the previous attention mechanism where we used the decoder hidden state to compute the context vector, here we only use the input hidden states. This is achieved through two linear transformations shown below

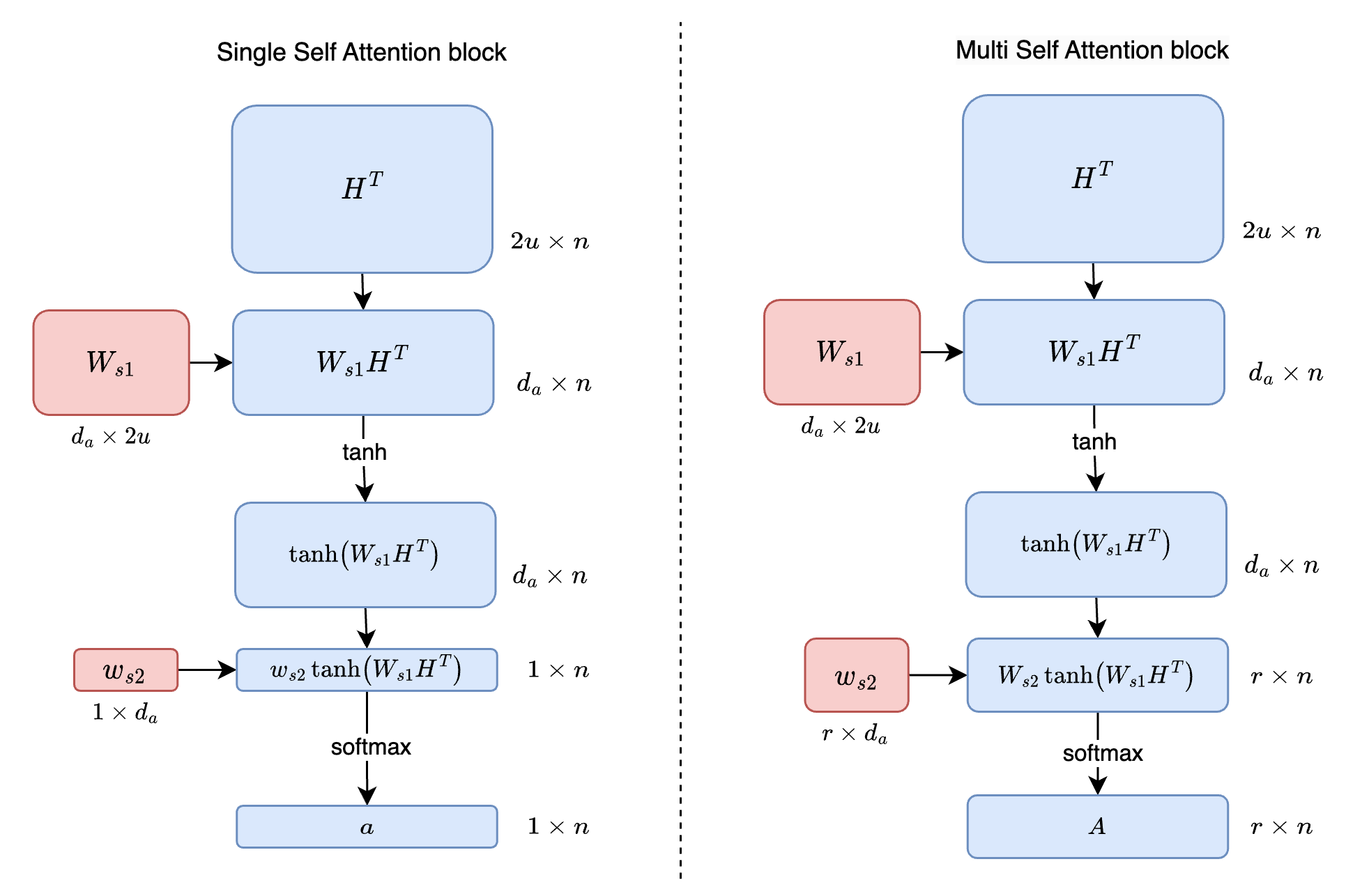
Fig. Self attention mechanism for single and multiple annotation vector

The image to the left above shows the transformations for a single annotation vector a and the image to the right is for the annotation matrix A. The only difference between the two is the we use vector \(w_{s2}\) for single attention and matrix \(W_{S2}\) for multiple attention to focus on different parts of the sentence. This is represented by the following equations in the paper

\begin{equation} a = softmax(w_{s2}\ tanh(W_{s1}\ H^T)) \end{equation}

\begin{equation} A = softmax(W_{s2}\ tanh(W_{s1}\ H^T)) \end{equation}

The dimensions of the output during the above transformations are shown in the fig above. We get the embedding vector m (\(1 \times 2u\)) and embedding matrix M (\(r \times 2u\)) by taking the weighted sum of H using a and A respectively. To solve for redundancy problems the paper mentions a penalization term (section 2.2) which we will not cover here. This builds up to the seminal paper Attention Is All You Need which proposed the Transformer, a network architecture based only on attention mechanism.

Transformers

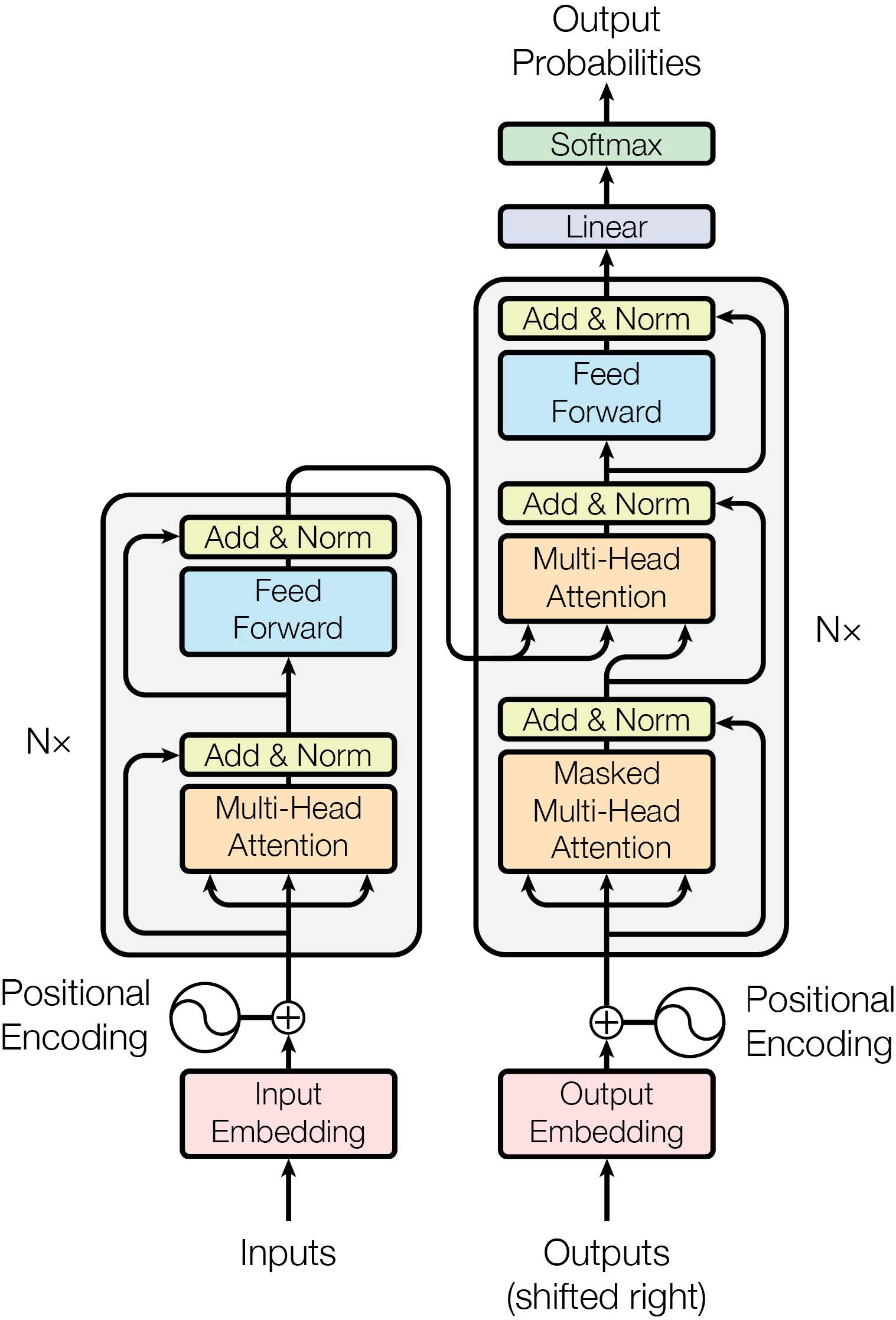
Introduced in 2017, this topic needs no introduction so we will get right to it. Using our understanding of the attention mechanism and sequence-2-sequence networks covered so far, we look at the Scaled Dot-Product Attention and Multi-Head Attention (orange block in the fig. below) used in Transformers. Self-attention, as defined is an attention mechanism relating different positions of a single sequence in order to compute a representation of the sequence.

Fig. Transformer architecture from

Scaled Dot-Product Attention

The attention function (shown below) can be defined as mapping a query and a set of key-value pairs to an output where the output is a weighted sum of the values with weights computed by a function of the query and corresponding key.

\begin{equation} Attention(Q, K, V) = softmax(\frac{QK^T}{\sqrt{d_k}})V \end{equation}

The inputs are key and query vectors of dimension \(d_k\) and value of dimension \(d_v\). The following operations are performed:

  • Take the dot product of \(Q\) and \(K^T\)
  • Scale it by \(\frac{1}{\sqrt{d_k}}\)
  • Apply softmax to the scaled dot product to obtain weights
  • Compute linear combination of (\(V\)) and weights
Scaled Dot-Product Attention

How do you generate the \(Q, K, V\) matrices? The output from the embedding layer is \(n\) tokens of size \(d_{model}\). To convert to \(d_k\) we linearly project the embedding vector by a matrix of size \(d_{model} \times d_k\) shown below. In practice, we group the input vectors before linearly projecting them to obtain the \(Q, K, V\) matrices.

Generating Q, K and V from input embedding

Multi-Head Attention

Here we have multiple (\(h\) ie. number of heads) Scaled Dot-Product Attention blocks running in parallel. Thus we project the queries, keys and values \(h\) times with different learned linear projections to \(d_k, d_k, d_v\) dimensions. This is shown in the figure above.

\begin{equation} head_i = Attention(QW_i^Q, KW_i^K, VW_i^V) \end{equation}

where \(W_i^Q \in \mathbb{R}^{d_{model} \times d_k}\), \(W_i^K \in \mathbb{R}^{d_{model} \times d_k}\) and \(W_i^V \in \mathbb{R}^{d_{model} \times d_v}\). Depending on \(h\) (number of heads), \(d_k = \frac{d_{model}}{h}\). In the paper, \(h = 8\) and \(d_k = d_v\).

Once you have the outputs from each head, you concatenate them and perform a linear projection as follows

\begin{equation} MultiHead(Q, K, V) = Concat(head_1, …, head_h)W^O \end{equation}

where \(W^O \in \mathbb{R}^{hd_v \times d_{model}}\). This is shown below

Multi-Head Attention
  • Since each head only works on part of the input, the total computational cost is same as that of single-head attention with full dimensionality.
  • To prevent the leftward flow of information and to preserve the auto-regressive property, all the illegal connections are set to \(-\infty\) pre-softmax.

For additional details regarding positional encoding, encoder-decoder, training etc. please refer to .

Conclusion

The domain of attention and transformer based architectures is a rapidly evolving field with new techniques published at lightning speed so it’s impossible to cover everything everywhere all at once. Certainly read the papers mentioned in the references below to dive deeper on this topic and I hope this read has been worth your time. Please do reach out with feedback and questions if any. Thanks!